 |
| Oryginalny Saper z Windows 7. Ciekawostka: wersja z Windows 8 posiada tryb przygodowy :) . |
Postaram się w tym wpisie przybliżyć, zarówno zasady gry, jak i kod, który umożliwił mi zrobienie na potrzeby tego wpisu dość ubogiego klona.
Kod starałem się napisać w miarę jak najprościej i zarazem starałem unikać się jak tylko to możliwe obiektowego programowania. Pozwoli to na bezproblemowe przepisanie aplikacji pod inne języki, które pod tym względem mogą być mniej zaawansowane niż Java. Także odpuściłem sobie zaprogramowanie paru rzeczy znajdujących się w oryginale, wychodząc z założenia, że najważniejsza jest sama mechanika gry.
Kod źródłowy wraz ze skompilowaną wersją znajduje się pod tym linkiem: [klik]
W dalszej części wpisu znajduje się opis kodu oraz zasad gry.
Krótko o zasadach Sapera
Jeżeli nigdy nie grałeś w Sapera, bądź nigdy nie rozumiałeś o co w tej grze chodzi, oto proste wyjaśnienie.
Po odpaleniu gry dostajemy planszę pełną przycisków, gdzie pod niektórymi z nich znajdują się miny. Po naciśnięciu przycisku, pod którym nic nie było, dostaniemy informację ile min znajduje się wokół. Na podstawie takiej informacji, musimy zgadnąć gdzie znajdują się miny. Gdy odgadniemy wszystkie pozycje, gra kończy się zwycięstwem. W przeciwnym wypadku, gdy klikniemy na polu pod którym kryje się mina, przegrywamy. Poniższe rysunki przedstawiają tą zasadę: (dla uproszczenia miny oznaczam literą M)
 |
| Tutaj dwie miny. Warto zwrócić uwagę, jak jedynki mogą nam szczegółowo podpowiedzieć rozmieszczenie min. |
 |
| Analogicznie jak w powyższych przypadkach, jednak tu mamy 3 miny. Oczywiście wokół jednego pola z liczbą może być nawet 8 min, jednak nie chcę pokazywać tutaj każdej możliwej ilości min. |
Żeby w pełni poznać tą mechanikę, polecam po prostu włączyć Sapera i grać. Ewentualnie, by zrozumieć rozkład tych cyfr, można też pobrać mój klon, w którym pod środkowym przyciskiem myszy umieściłem drobny cheat pokazujący zawartość planszy.
Gdy już zrozumieliśmy zasady, można bez problemu przejść do zaprogramowania gry.
Rozpoczynamy programowanie - czyli zaplanowanie działania gry
Pierwsze co trzeba zrobić, to rozplanować działanie gry. Przez to mam na myśli, jak będą przechowywane dane, jak będą wyświetlane oraz w dalszej kolejności, na jakie metody (funkcje, procedury) rozdzielimy akcje wykonywane przez naszą aplikację.
Wizja, którą tu przedstawię jest lekko inspirowana przedstawioną w książce "Delphi 4. Praktyka programowania" autorstwa Marco Cantu (ISBN 83-7158-186-6). Mianowicie, nasza plansza będzie dwuwymiarową tablicą intów, w której liczby 0-8 będą oznaczać ilość otaczających pole min, -1 minę, -2 minę odgadniętą przez gracza, -3 nieudane odgadnięcie miny (w oryginale książkowym była tablica typu char).
Całość będzie reprezentowana graficznie przez zwykłe Javowskie przyciski (tutaj nie tak do końca, wyjaśnię później), które także będą przechowywane w tablicy dwuwymiarowej, w taki sposób, że współrzędne będą się pokrywać.
Wygrana będzie determinowana przez to, czy użytkownik oznaczył prawym przyciskiem myszy wszystkie pola, gdzie znajdują się miny, jednocześnie nie oznaczając pół pod którymi są liczby. W tym celu zastosuję dwie zmienne: typu int do przechowywania ilości znalezionych min oraz typu boolean w celu sprawdzenia, czy użytkownik nie zaznaczył złego pola. Jest to nieco inny sposób niż w Windowsowym Saperze - tam nie musimy oznaczać min, wystarczy że odkryjemy wszystkie wolne od nich pola. Nie jest to trudne do zaprogramowania, nawet oba sposoby można bez problemu połączyć, jednak takie modyfikacje pozostawiam już Tobie.
Rozplanowanie akcji - za podstawowe, które przewidziałem na samym początku powstawania gry uznałem (pomijam w tym momencie argumenty metod):
Mówiąc krótko - metoda nextInt(n) klasy Random zwraca nam losową liczbę z przedziału [0;n).
Wracając do wcześniejszego kodu. Gdy już wylosowaliśmy współrzędne, mamy już potencjalnego kandydata gdzie można by postawić minę. Musimy jednak sprawdzić, czy rzeczywiście możemy tam postawić minę. Jeżeli tak, to zmieniamy wartość pola na -1 (mina) i zmniejszamy licznik. Jako, że przypadków kiedy nie możemy dać miny jest wiele, to w celu uproszczenia kodu posłużymy się tu pomocniczą metodą canPutTheMine(x,y) typu boolean. Opiszę ją jednak po obliczaniu ilości min, gdyż będziemy się wspomagać metodami pomocniczymi z tejże części.
Całość będzie reprezentowana graficznie przez zwykłe Javowskie przyciski (tutaj nie tak do końca, wyjaśnię później), które także będą przechowywane w tablicy dwuwymiarowej, w taki sposób, że współrzędne będą się pokrywać.
Wygrana będzie determinowana przez to, czy użytkownik oznaczył prawym przyciskiem myszy wszystkie pola, gdzie znajdują się miny, jednocześnie nie oznaczając pół pod którymi są liczby. W tym celu zastosuję dwie zmienne: typu int do przechowywania ilości znalezionych min oraz typu boolean w celu sprawdzenia, czy użytkownik nie zaznaczył złego pola. Jest to nieco inny sposób niż w Windowsowym Saperze - tam nie musimy oznaczać min, wystarczy że odkryjemy wszystkie wolne od nich pola. Nie jest to trudne do zaprogramowania, nawet oba sposoby można bez problemu połączyć, jednak takie modyfikacje pozostawiam już Tobie.
Rozplanowanie akcji - za podstawowe, które przewidziałem na samym początku powstawania gry uznałem (pomijam w tym momencie argumenty metod):
- wygenerowanie planszy - void generateField()
- odsłonięcie pola - void showField()
- oznaczenie, że pod przyciskiem znajduje się mina - void setGuess()
Reszta napisanych przeze mnie metod, to metody pomocnicze. Powyższym poświęcę dalsze części tego wpisu.
Programujemy wygenerowanie planszy
Jak można się domyśleć, jest to absolutna podstawa, bez której nie możemy przeprowadzić w ogóle rozgrywki. Samo generowanie postanowiłem podzielić na trzy części: deklaracja zmiennej tablicowej z planszą, rozłożenie min, obliczenie ilości otaczających min. Pierwszej z nich nie będę tu szerzej rozpisywać, gdyż jest to jedna linijka totalnych podstaw programowania. Dalsze części to natomiast zagadnienie dużo ciekawsze.
Rozłożenie min na planszy
Wbrew pozorom mogłoby się to wydawać całkiem prostym zadaniem - parę razy wylosować pozycję i umieścić tam minę. W dużej mierze, tak to właśnie się odbywa, jednak są przypadki, kiedy miny w danym miejscu postawić nie możemy. Na razie, skupmy się na tej podstawie.
Oto gotowy kod, który będę opisywać:
int i=minesCount; while (i>0){ int x=random(fieldWidth); int y=random(fieldHeight); if (canPutTheMine(x,y)){ field[x][y]=-1; i--; } }
Podstawą dla nas jest pętla, która będzie wykonywać się tak długo, aż min na planszy będzie tyle ile zaplanowaliśmy. Ja osobiście wolałem podejść do tego licząc od tyłu, stąd najpierw zmiennej i przypisujemy ilość min, a warunkiem pętli jest "tak długo jak i jest większe od 0". W tym momencie jednak, można zadać pytanie - skoro odliczamy, to dlaczego nie pętla for? Odpowiadam - można użyć pętli for. Jednak, licznik dekrementujemy tylko w przypadku gdy minę położyliśmy. Stąd, przynajmniej dla mnie, wygodniej jest zrobić pętle while, w której zmniejszanie wartości licznika ustawiamy w interesującym nas miejscu, a nie na stałe po ukończeniu przebiegu.
Gdy już jesteśmy w pętli, to trzeba wylosować jakąś pozycję, na której spróbujemy postawić minę. Jak widać, posłużyłem się tutaj pomocniczą metodą, której kod wygląda następująco:
Gdy już jesteśmy w pętli, to trzeba wylosować jakąś pozycję, na której spróbujemy postawić minę. Jak widać, posłużyłem się tutaj pomocniczą metodą, której kod wygląda następująco:
private int random(int max){ Random rand = new Random(); return rand.nextInt(max); }
Wracając do wcześniejszego kodu. Gdy już wylosowaliśmy współrzędne, mamy już potencjalnego kandydata gdzie można by postawić minę. Musimy jednak sprawdzić, czy rzeczywiście możemy tam postawić minę. Jeżeli tak, to zmieniamy wartość pola na -1 (mina) i zmniejszamy licznik. Jako, że przypadków kiedy nie możemy dać miny jest wiele, to w celu uproszczenia kodu posłużymy się tu pomocniczą metodą canPutTheMine(x,y) typu boolean. Opiszę ją jednak po obliczaniu ilości min, gdyż będziemy się wspomagać metodami pomocniczymi z tejże części.
Obliczanie ilości sąsiadujących min
Jest to bardzo proste zagadnienie, nad którym polecam zastanowić się samemu. Znając zasady sapera, wiemy, że niektóre pola przechowują liczbę oznaczającą ile min jest wokół nich. Może być ich od 0 do 8. Aby je wyliczyć, wystarczą proste pętle for. Zacznijmy jednak od kodu, w którym przelecimy całą planszę w celu obliczenia interesującej nas wartości:
for (i=0; i<fieldWidth; i++) for (int j=0; j<fieldHeight; j++) if (field[i][j]!=-1) field[i][j]=countMines(i,j);
Nie ma tu większej filozofii - obie pętle for to najzwyklejsze przechodzenie tablicy dwuwymiarowej - w tym przypadku, z góry na dół. Natomiast w kodzie wewnętrznej pętli musimy sprawdzić, czy pod sprawdzanym przez nas polu nie ma przypadkiem miny. Jak nie ma, to dopiero wtedy przechodzimy do wyliczenia ilości sąsiadujących min. W tym celu posługuję się metodą pomocniczą countMines(x,y). Wygląda ona następująco:
private int countMines(int x, int y){ int mines=0; for (int i=x-1; i<=x+1; i++) if (i>=0 && i<fieldWidth) for (int j=y-1; j<=y+1; j++) if (j>=0 && j<fieldHeight) if (i!=x || j!=y) if (field[i][j]==-1 || field[i][j]==-2) mines++; return mines; }
- Dla kolumn od x-1 do x+1
- Jeżeli nasza pozycja jest na planszy (czyli jest większa bądź równa 0 i mniejsza od szerokości planszy) to przechodzimy dalej
- Dla wierszy od y-1 do y+1
- Jeżeli nasza pozycja jest na planszy (tak jak wcześniej, z tą zmianą, że mniejsza od wysokości planszy) to przechodzimy dalej
- Jeżeli pozycja jest różna od wyjściowego x,y, to przechodzimy dalej. Dla jasności - zastosowanie || (or/lub) w warunku bierze się z praw deMorgana, wedle których ~(x /\ y) jest równoważne ~x \/ ~y
- Jeżeli pole zawiera minę (-1) lub odgadniętą minę (-2) to zwiększ licznik.
Ostatecznie, kod metody wygląda następująco:
private void generateField(){ field = new int[fieldWidth][fieldHeight]; int i=minesCount; while (i>0){ int x=random(fieldWidth); int y=random(fieldHeight); if (canPutTheMine(x,y)){ field[x][y]=-1; i--; } } for (i=0; i<fieldWidth; i++) for (int j=0; j<fieldHeight; j++) if (field[i][j]!=-1) field[i][j]=countMines(i,j); }
Rozmieszczania min ciąg dalszy
Teraz możemy wrócić do zagadnienia rozmieszczania min, a dokładniej, do metody pomocniczej canPutTheMine(x,y). Jak wspomniałem wcześniej, jest wiele przypadków kiedy nie możemy umieścić miny na danym polu. Pierwszy, najbardziej oczywisty - na polu znajduje się już mina. Najczęściej, na tym kończy się u wielu. Przed napisaniem tego wpisu przeczytałem sporo przykładów zamieszczonych w sieci i każdy ograniczał się do sprawdzenia tylko tego. Co prawda, na małych planszach typu 9x9 z 10 minami, jest to zupełnie wystarczające, jednak im wyższe wartości, to zaczyna się pojawiać problem - położenia pewnych min nie da się przewidzieć. Postaram się to zobrazować na poniższym obrazku:
Pozornie wydaje się, że wszystko jest w porządku. Pola oznaczają nam ile min jest przy nich i możemy bez problemu zgadnąć tak 8 min. Jednak, mina oznaczona czerwonym kółkiem nie jest w żaden sposób do przewidzenia. Gracz nie ma prawa wiedzieć, że tam jest mina, ponieważ nie wskazuje na to żadna liczba. Jest to sytuacja błędna, która w grze zdarzyć się nie może - w sąsiedztwie każdej miny musi być przynajmniej jedno pole z liczbą. Analogicznie jest w poniższych sytuacjach, gdy mamy obok siebie 6 lub 4 miny tylko, jednak są one przy krawędzi lub na rogu planszy:
Nie posiadamy żadnej możliwości odgadnięcia min oznaczonych czerwonymi kółkami, więc ich położenie jest błędne. Dlatego też stwierdziłem, że warto napisać oddzielną metodę do sprawdzania czy można postawić minę w danym miejscu. Prezentuje się ona następująco:
private boolean canPutTheMine(int x, int y){ if (field[x][y]==-1) return false; if (!minesCheck(x,y)) return false; for (int i=x-1; i<=x+1; i++) if (i>=0 && i<fieldWidth) for (int j=y-1; j<=y+1; j++) if (j>=0 && j<fieldHeight) if (i!=x || j!=y){ field[x][y]=-1; if (!minesCheck(i,j)){ field[x][y]=0; return false; } field[x][y]=0; } return true; }
W pierwszym warunku, sprawdzamy wspomnianą przeze mnie najbardziej podstawową rzecz - czy czasem na podanym polu nie znajduje się już mina. Jeżeli znajduje się - zwracamy fałsz.
Kolejno postanowiłem sprawdzać czy nie trafimy w miejsce gdzie nie dosięgnie nas żadna liczba, oraz czy nie sprawimy takiej sytuacji którejś z postawionych już min. Posłużę się tutaj pomocniczą metodą minesCheck(x,y). O niej za chwilę opowiem bardziej szczegółowo. Jeżeli chodzi o pętlę for, to odbywa się tam sprawdzenie czy nie zasłonimy którejś z sąsiadujących z polem min. Jak widać, rozkład pętli i warunków jest analogiczny do tego, który użyłem przy zliczaniu min i jest to nie pierwszy przypadek, gdzie powielimy to. Warto jednak przyjrzeć się na sam koniec tego - sprawdzanemu polu ustawiamy natomiast wartość -1, czyli minę. Dlaczego? Ponieważ w tym miejscu będziemy "symulować" sytuację jakby mina była już tu umieszczona. Nasza metoda pomocnicza wtedy zadziała dla sąsiadujących min bez konieczności dodatkowych przeróbek. Trzeba jednak pamiętać, żeby przed wyjściem ze sprawdzania, przywrócić wartość z powrotem na 0.
Wracając do metody minesCheck(x,y), jej kod prezentuje się następująco:
private boolean minesCheck(int x, int y){ if (countMines(x,y)==8) return false; if ((x==0 || x==fieldWidth-1) && (y==0 || y==fieldHeight-1)) if (countMines(x,y)==3) return false; if (x==0 || x==fieldWidth-1 || y==0 || y==fieldHeight-1) if (countMines(x,y)==5) return false; return true; }
Drugi przypadek jest wtedy, gdy mina jest w narożniku i dostęp do niej zostaje przyblokowany przez trzy otaczające ją. Są tylko cztery takie miejsca i zostały odzwierciedlone w warunku. Dla uproszczenia, zamiast wyliczać każdą możliwą pozycję jako oddzielny warunek, zauważamy, że są tylko dwie możliwości dla pozycji x i dwie możliwości dla pozycji y, co odwzorowujemy w kodzie.
Trzeci przypadek można nazwać bardziej ogólną wersją poprzedniego. Tym razem sprawdzamy czy pole znajduje się przy jednej z czterech krawędzi. Jeżeli tak, to złą sytuacją jest gdy zostaje otoczone przez 5 min.
Jak widać, warunki te pokryły się z sytuacjami opisanymi na rysunkach. Jak wspomniałem wcześniej, dzięki umieszczeniu ich w oddzielnej metodzie, możemy wywołać sprawdzenie nie tylko dla pola na którym aktualnie kładziemy minę, ale także dla sąsiadujących. Dzięki temu możemy być pewni, że nie będzie nieprawidłowych sytuacji.
Dodatkowo, można dopisać inny warunek - żeby mina nie wygenerowała się w jakimś zadanym polu. Może się to przydać, gdy chcemy wprowadzić taki system jak jest w oryginale, czyli, że plansza tak na prawdę generuje się po pierwszym odsłonięciu pola. Dzięki temu, nie wprawimy gracza w irytację game overem po jednym kliknięciu :) . Nie zostało to przewidziane w tym przykładzie, jednak nie jest to skomplikowana zmiana i każdy programista bez problemu powinien sobie z nią poradzić.
Odsłonięcie pola
Gdy zaprogramowaliśmy już generowanie pola, zostały przed nami jeszcze dwa aspekty - odsłonięcie pola i oznaczanie min. Zajmijmy się tym pierwszym.
Jest to domyślna akcja w saperze, która znajduje się pod lewym przyciskiem myszy. Zanim jednak przejdę do szczegółów tego, wcześniej wspomnę o jednej rzeczy - przyciskach. Jak naciśnie się na przycisk, mogę dostać bez problemu informację, który przycisk to zrobił. Jednak, nie znam jego współrzędnych, pod którymi się kryje w tablicy przycisków. Są różne sposoby na rozwiązanie tego problemu - najprostszym i chyba najgorszym byłoby wyszukiwanie po tablicy przycisk po przycisku, który to ten wciśnięty. Ja jednak postanowiłem wykorzystać dobrodziejstwa programowania obiektowego i stworzyłem własny przycisk. To znaczy, nie tak do końca własny - postanowiłem rozszerzyć klasę JButton o dodatkową informację - położenie na planszy. Stąd wzięła się klasa MyButton, która wygląda następująco:
import javax.swing.JButton; public class MyButton extends JButton { private final int fieldX; private final int fieldY; public MyButton(int x, int y){ super(); fieldX=x; fieldY=y; } public int getFieldX(){ return fieldX; } public int getFieldY(){ return fieldY; } }
private void showField(MyButton button){ int x = button.getFieldX(); int y = button.getFieldY(); if (field[x][y]!=-2 && field[x][y]!=-3){ if (field[x][y]==-1){ button.setText("M"); JOptionPane.showMessageDialog(frame, "Game over!"); frame.dispose(); } else{ button.setEnabled(false); button.setText(Integer.toString(field[x][y])); if (field[x][y]==0) showZeros(x,y); } } }
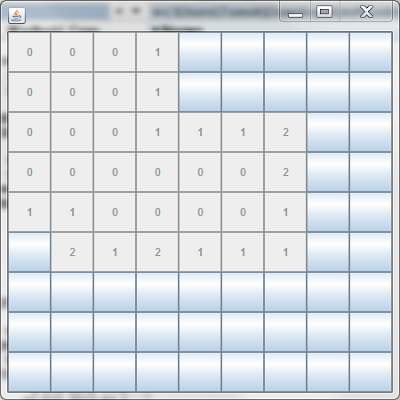
Jeżeli pod przyciskiem nie było miny, to blokujemy przycisk oraz ustawiamy jako jego tekst ilość sąsiadujących z polem min. Warto tu zauważyć, że w Saperze, gdy klikniemy na pole niesąsiadujące z minami, automatycznie odsłaniają się wszystkie takie pola wokół, co zostało całkiem ładnie pokazane na screenie na samym początku wpisu (osiągnąłem to jednym kliknięciem). Stwierdziłem, że najlepiej jest to zapisać w oddzielnej metodzie, stąd zamiast żadnych pętli, dajemy warunek, czy pole jest równe 0, jeśli tak, to wywołanie showZeros(x,y). Wygląda ono następująco (tabulatory zamieniłem na spację dla zwiększenia czytelności):
private void showZeros(int x, int y){ if (field[x][y]==0) for (int i=x-1; i<=x+1; i++) if (i>=0 && i<fieldWidth) for (int j=y-1; j<=y+1; j++) if (j>=0 && j<fieldHeight) if (i!=x || j!=y){ fieldButtons[i][j].setText(Integer.toString(field[i][j])); if (fieldButtons[i][j].isEnabled()){ fieldButtons[i][j].setEnabled(false); showZeros(i,j); } } }
Tym samym skończyliśmy zaprogramowanie akcji odsłonięcia przycisku. Została nam już tylko jedna część podstawowej mechaniki do zaprogramowania.
Oznaczanie min
Oznaczanie przez gracza, gdzie znajduje się mina, to akcja która w Saperze znajduje się pod prawym przyciskiem myszy. Stawiamy wtedy na planszy flagę, która oznacza, że w tym miejscu jest mina. My ten mechanizm nieco uprościmy i zarazem rozszerzymy. Uproszczenie będzie polegać na tym, że w oryginale oprócz flagi możemy postawić także znak zapytania - rzecz nie mająca znaczenia w rozgrywce, a służącą tylko za pomoc dla gracza; my tego elementu nie implementujemy. Za to rozszerzenie opisałem już wcześniej - wygrana będzie determinowana przez postawienie flag na minach. Dość opisywania, przejdźmy do kodu:
private void setGuess(MyButton button){ int x = button.getFieldX(); int y = button.getFieldY(); if (button.isEnabled()){ if (field[x][y]==-1){ field[x][y]=-2; button.setText("!"); minesFound++; if (minesFound==minesCount && !isWrong){ JOptionPane.showMessageDialog(frame, "You've won!"); frame.dispose(); } } else if (field[x][y]==-2){ field[x][y]=-1; button.setText(""); minesFound--; } else if (field[x][y]==-3){ field[x][y]=countMines(x,y); isWrong=false; button.setText(""); } else { field[x][y]=-3; button.setText("!"); isWrong=true; } } }
Pierwsze dwie linijki pomijam, omawiałem je przy akcji lewego przycisku. Natomiast to, co zaciekawi wielu znajduje się w pierwszym warunku - po co sprawdzać czy przycisk jest aktywny w akcji naciśnięcia przycisku? Odpowiedź brzmi prosto - w Javie blokada przycisku działa tylko na lewy przycisk myszy :) . Prawdopodobnie tego elementu w innych językach w ogóle nie trzeba będzie implementować. Jednak, następne warunki są już kwintesencją tego co chcemy tu zrobić i reprezentują cztery możliwe sytuacje, na które możemy się natknąć. Mimo, że część programistów w tej części użyłaby konstrukcji switch...case, ja wolałem pozostać przy tradycyjnych ifach.
Pierwszy warunek sprawdza, czy pod przyciskiem znajduje się mina. Jeżeli tak, to przestawiamy minę, na odgadniętą minę (-2), a przyciskowi ustawiamy jako tekst wykrzyknik. Inkrementujemy też licznik znalezionych min, co przyda się dalej. Następnie natomiast mamy sprawdzenie, czy ilość odgadniętych min (minesFound) jest równa liczbie min na planszy (minesCount), oraz czy gracz ani razu przy oznaczaniu nie pomylił się (isWrong). Jeżeli warunki są spełnione, mamy akcję wygranej gry, która u mnie jest dialogiem i wyłączeniem programu. Podobnie jak wcześniej przy akcji przegranej - warto pomyśleć tutaj nad jakimś restartem, a także np. tablicą najlepszych wyników.
Drugi warunek sprawdza, czy pod przyciskiem znajduje się znana mina. Oznacza to dokładnie tyle, że już raz został naciśnięty na danym polu prawy przycisk myszy i użytkownik chce cofnąć swoją decyzję. W takim razie, musimy zmniejszyć zdekrementować licznik znalezionych min, przywrócić na planszy zwykłą minę i zmienić tekst przycisku na pusty.
Trzeci warunek jest analogiczny do poprzedniego, jednak zmieniamy nieudane trafienie (-3) na pusty przycisk. Z racji, że przy nieudanym trafieniu nadaliśmy naszemu polu wartość -3, musimy na polu obliczyć jeszcze raz, z iloma minami sąsiaduje. Musimy też ustawić isWrong na false.
Ostatni przypadek, to tak na prawdę akcja kiedy naciskamy prawy przycisk na polu, gdzie nie znajduje się mina. Wtedy stawiamy znak zapytania, jednak nie inkrementujemy licznika min, a za to ustawiamy zmienną isWrong na true. Dzięki temu, tak długo jak użytkownik pozostawi tutaj "flagę", tak długo nie będzie mógł wygrać gry.
Tym samym zaprogramowaliśmy właśnie wszystkie podstawowe działania w grze. Jedyne co nam zostało to interfejs i ewentualne dodatkowe akcje. Te opowiem już w skrócie poniżej.
Najlepszy przyjaciel testera - cheat
Żeby przetestować, czy nasza plansza generuje się prawidłowo, warto zaprogramować cheat, który odsłoni nam całą planszę. Dzięki temu możemy szybko sprawdzać, czy miny dobrze się rozmieszczają, czy obliczenia min są dobre, itd. Gdy piszemy grę od podstaw, bez gotowych poradników takich jak ten, jest to niezwykle przydatne. Wygląda to następująco u mnie:
private void cheat(){ for (int i=0; i<fieldWidth; i++) for (int j=0; j<fieldHeight; j++){ String text = Integer.toString(field[i][j]); if (text.equals("-1") || text.equals("-2")){ text="M"; fieldButtons[i][j].setBackground(Color.RED); } else if (text.equals("-3")) text=Integer.toString(countMines(i,j)); fieldButtons[i][j].setText(text); //fieldButtons[i][j].setText(fieldButtons[i][j].getFieldX()+","+fieldButtons[i][j].getFieldY()); } }
Natomiast zostawiłem jedną linijkę zakomentowaną. Gdy odkomentujemy ją, zamiast zawartości pola, dostaniemy współrzędne pod jakimi jest dany przycisk. Wbrew pozorom głupie, jednak przy testach bardzo pomogło, gdyż jak się okazało, w trakcie pisania popełniłem głupi błąd, w wyniku którego osie x i y były ze sobą zamienione :) . Nie było to widoczne przy normalnej grze na kwadratowej planszy, jednak na prostokątnych powodowało bardzo dziwne błędy, a linijka ta zaoszczędziła mi kilka godzin zastanawiania się, czemu gra źle działa.
Jak wcześniej wspomniałem, cheat ten znajduje się u mnie pod środkowym przyciskiem myszy. Przyznam, że jest to z czystego lenistwa - nie chciało mi się zaprogramowywać klawiatury, a gdy miałem akcje poszczególnych przycisków myszy, to czemu by nie użyć też środkowego w jakimś celu...
Interfejs oraz Javowe szczegóły
Pod tą krótką nazwą skrywa się w zasadzie coś, co ciężko tak nazwać. Tak na prawdę w kodzie, który zamieściłem do ściągnięcia wyżej z bitbucketa, nie znajduje się zaprogramowane nic, poza wyświetleniem przycisków. Ciekawa i na pewno przydatna dla niektórych będzie metoda jak je rozmieściłem - ustawiłem ramkę aplikacji by posiadała layout GridLayout. Dzięki niemu, elementy rozmieszczane są jak w tablicy o podanej ilości wierszy i kolumn. Zapewniło mi to to, że nie musiałem przejmować się rozmieszczeniem przycisków po planszy, tylko tworzyłem je po kolei, a one same dodają się jak powinny.
Prawdziwą trudnością (a raczej przeszkodą) w Javie jest doprowadzenie do działania innych przycisków myszy niż lewy. W tym celu musiałem nadać przyciskowy nowy MouseListener, w którym określam wszystkie akcje możliwe do zrobienia myszką. Jednak w innych językach jest zazwyczaj prościej.
Kolejną dopisaną przeze mnie rzeczą, jest obsługa argumentów. Dzięki temu, wpisując w konsoli
mines.jar 20 10 100
Kodów powyższych rzeczy nie zamieszczam, ponieważ nie są to najważniejsze rzeczy w grze, a udostępniam kod źródłowy. Warto jednak elementy te napisać samemu i dopasować pod swoje potrzeby. Gra w postaci napisanej przeze mnie jest bardzo prymitywna i oferuje tylko podstawową funkcjonalność, a warto tutaj samemu przemyśleć kwestię co ulepszyć, co dodać, co zmienić.
Efekt końcowy u mnie prezentuje się następująco:
Mam nadzieję, że u Ciebie będzie ładniej :) .




Brak komentarzy:
Prześlij komentarz